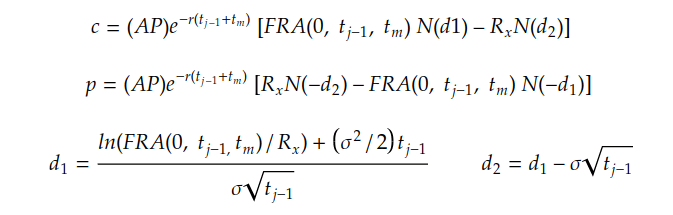Interest rate options are options based on interest rates, where the underlying asset is a reference interest rate, typically in the form of a Forward Rate Agreement (FRA). For instance, an interest rate call option on a 3-month MRR (market reference rate) with 9 months to expiration would have a 3-month FRA rate expiring in 9 months as its underlying interest rate.

Similar to futures options, the BSM model cannot be directly applied to price interest rate options because the dynamics of interest rates differ significantly from those of stock prices. For instance, stock prices follow a Geometric Brownian Motion (GBM), which results in a lognormal distribution. In contrast, interest rates exhibit a mean-reverting pattern, leading to variable volatility, whereas the BSM model assumes constant volatility. This difference in volatility behaviour makes the BSM model unsuitable for pricing interest rate options.

For interest rate options, the Black model, introduced in the previous blog post, is more suitable. Below is the Black model formula adjusted for pricing interest rate options.

Here, I will only focus on the terms in the Black model formula that are unique to interest rate option pricing. For more details on the complete formula, please refer to the previous two blog posts.

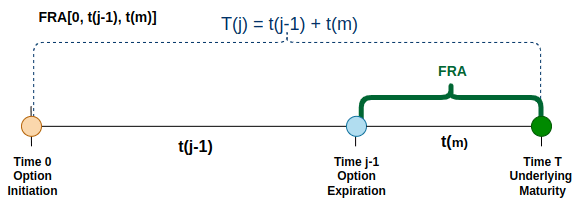
For an interest rate option, the underlying is an FRA contract. The fixed rate of this FRA at time 0 can be denoted as FRA[0, t(j-1), t(m)], where the option expires at time t(j-1) and the underlying matures at time t(j-1)+t(m). R(x) denotes the strike rate at the option expiration.

As interest rates are typically settled in arrears, i.e., interest payments are made at the maturity of the underlying deposits (time t(j-1) + t(m)), the present value of the option payoffs is calculated by discounting from the underlying expiration time, not the option expiration time.

In addition, since the interest rates used in the formula are annualised, it is important to adjust for the time period when calculating the value or pricing of the FRA option by reflecting the FRA’s specific period.

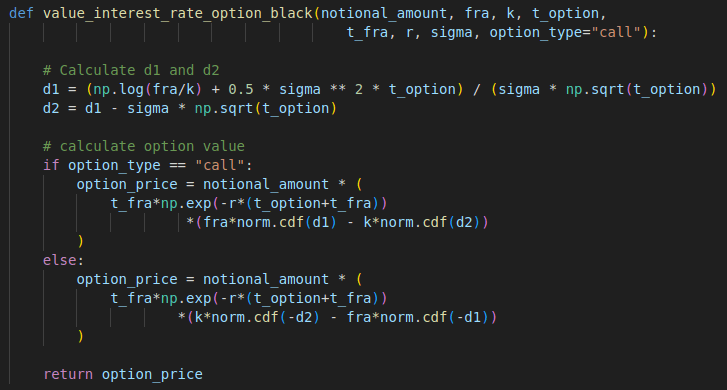
Here is the Python code implementation. Since I have used the “year” as the time period unit for both the option period and the FRA period, we can use the FRA period as the “AP” (accrued period) in the formula above to adjust the annualised interest rate. This allows for the scaling of the annualised rate to the appropriate rate for the FRA period.

Full Code – Python

import numpy as np
from scipy.stats import norm

def value_interest_rate_option_black(notional_amount, fra, k, t_option, t_fra, r, sigma, option_type="call"):

    # Calculate d1 and d2
    d1 = (np.log(fra/k) + 0.5 * sigma ** 2 * t_option) / (sigma * np.sqrt(t_option))
    d2 = d1 - sigma * np.sqrt(t_option)

    # calculate option value
    if option_type == "call":
        option_price = notional_amount * (
            t_fra*np.exp(-r*(t_option+t_fra))
                     *(fra*norm.cdf(d1) - k*norm.cdf(d2))
        )
    else: 
        option_price = notional_amount * (
            t_fra*np.exp(-r*(t_option+t_fra))
                    *(k*norm.cdf(-d2) - fra*norm.cdf(-d1))
        )

    return option_price

notional_amount = 1000000
fra = 0.03
k = 0.025
t_option = 0.5
t_fra = 0.25
r = 0.0055
sigma = 0.15

call_price = value_interest_rate_option_black(notional_amount, fra, k, t_option, t_fra, r, sigma, option_type="call")
put_price = value_interest_rate_option_black(notional_amount, fra, k, t_option, t_fra, r, sigma, option_type="put")

print("Call Option on Interest Rate: "+str(call_price))
print("Put Option on Interest Rate: "+str(put_price))

Full Code – DolphinDB

def value_interest_rate_option_black(notional_amount, fra, k, t_option, t_fra, r, sigma, option_type="call"){

    // Calculate d1 and d2
    d1 = (log(fra/k) + 0.5 * pow(sigma, 2) * t_option) / (sigma * sqrt(t_option))
    d2 = d1 - sigma * sqrt(t_option)

    // calculate option value
    if (option_type == "call") {        
        option_price = notional_amount * (t_fra*exp(-r*(t_option+t_fra)) * (fra*cdfNormal(0, 1, d1) - k*cdfNormal(0, 1, d2)))
    }
    else {
        option_price = notional_amount * (t_fra*exp(-r*(t_option+t_fra)) * (k*cdfNormal(0, 1, -d2) - fra*cdfNormal(0, 1, -d1)))
    }

    return option_price
}

notional_amount = 1000000
fra = 0.03
k = 0.025
t_option = 0.5
t_fra = 0.25
r = 0.0055
sigma = 0.15

call_price = value_interest_rate_option_black(notional_amount, fra, k, t_option, t_fra, r, sigma, option_type="call")
put_price = value_interest_rate_option_black(notional_amount, fra, k, t_option, t_fra, r, sigma, option_type="put")

print("Call Option on Interest Rate: "+call_price)
print("Put Option on Interest Rate: "+put_price)

• Coding towards CFA