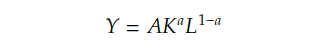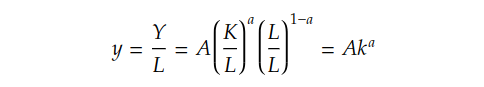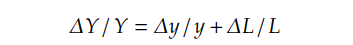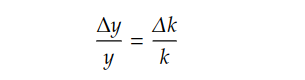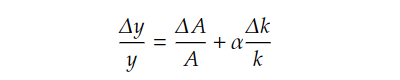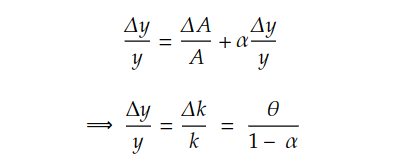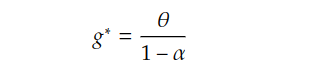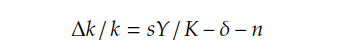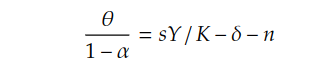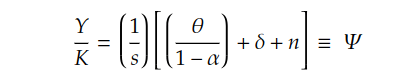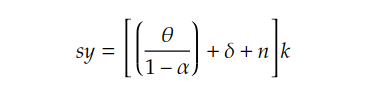This is another code-less blog post in my “Coding Towards CFA” series. The concepts of the Cobb-Douglas Production Function and the Neoclassical Growth Model are too important to skip, which is essential for building a strong foundation in economics and of course for pass on the CFA exam.

Neoclassical growth theory is a framework for understanding economic growth, analysing how the role of capital accumulation, labor force growth, and technological progress influence economic growth. The Neoclassical growth model is built on the Cobb-Douglas production function, which is one of the most widely used production functions in economics.

In this blog post, I will summarise the key insights I have learnt about these concepts.

Cobb-Douglas Production Function

First, a Production Function is a mathematical function that links the factors of production to the output of production. The Cobb-Douglas Production Function takes three factors into consideration: Capital Investment (K), Labour Investment (L), and Total Factor Productivity (A). The weights of capital investment and labour investment are the variables of the function. This means that capital and labour can be used in various combinations to produce output.

The Total Factor Productivity (TFP) is a multiplicative scale factor in the function, which implies a proportionate increase or decrease in output for any combination of capital and labour inputs. Therefore, TFP reflects the general level of productivity or technology in the economy. It is driven by the cumulative effects of factors such as scientific advances, applied research and development (R&D), and improvements in management methods.

The α denotes the share of GDP paid to the suppliers of capital, while (1−α) denotes the share of GDP paid to the suppliers of labour.

One important property of the Cobb-Douglas production function is constant returns to scale, which means that doubling all inputs (capital and labour) will double the output. For example,Y = F(2K, 2L). This property allows us to derive labour productivity, or output per worker, by dividing all independent and dependent variables by the total units of labour.

As the formula above shows, the output per worker is determined by the capital-to-labour ratio (k), i.e., the amount of capital available for each worker, the technology (TFP), and the share of capital in GDP (a).

The Cobb-Douglas production function can also be expressed in terms of growth rates, which forms the basis of Solow’s growth accounting equation. This equation shows that the growth rate of output is determined by the growth rate of technology, the growth rate of capital and the growth rate of labour.

Another way to measure the growth rate is through the labour productivity growth accounting equation. This equation states that the growth rate in potential GDP equals the sum of the long-term growth rate of labour productivity and the long-term growth rate of labour forces.

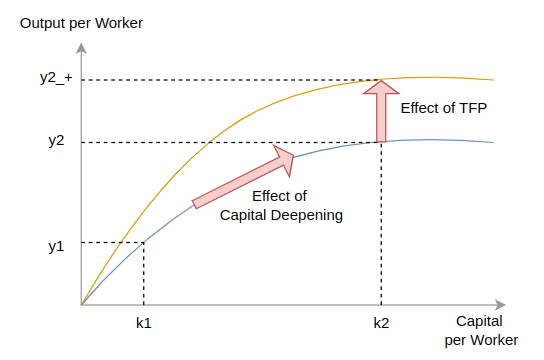
The labour productivity or output per worker (y) is determined by the capital per worker and the TFP. However, when capital per worker reaches a certain level, the effect of capital deepening (increasing capital per worker) diminishes. This reflects the second key property of the Cobb-Douglas production function: diminishing marginal productivity. This means that the additional output gained from each extra unit of input (capital or labour) will eventually decline. As a result, sustained growth in output per worker must primarily come from improvements in TFP.

Neoclassical Growth Model

The Neoclassical model builds on the Cobb-Douglas Production Function and aims to explore the following three factors’ effect on the long-term growth rate of output per capital:

• The technological growth rate  (g)
• The saving/investment rate (s)
• The population growth rate (n)

Steady-State Rate of Growth

The core of the Neoclassical Growth Model is based on the concept of the steady-state rate of growth. The steady state represents a long-run equilibrium where the output-to-capital ratio is constant, i.e., the capital per worker and output per worker grow at the same rate.

Based “Output per Work” form of Cobb-Douglas Production Function:

The growth rate of output per worker can be derived as:

As the growth rate of capital per worker equals the growth rate of output per worker at the steady state, then:

The θ denotes the growth rate of TFP and the α represents the share of GDP to capital. According to the labour productivity growth accounting equation, g is the long-term growth rate of labour productivity, which is determined by technology progress and the capital deepening.

The growth rate of capital per worker can be derived by considering the gross saving/investment, capital depreciation, and population growth, where the physical capital stock per worker in an economy will increase when gross investment rises or decrease when stock depreciation falls or labour supply rises.

s denotes the saving/investment rate, so sY represents gross investment. δ (delta) denotes the depreciation rate of the physical capital stock. n denotes the growth rate of the labour supply.

At the steady state, where the growth rate of capital per worker equals the growth rate of output per worker, we obtain the following equation:

After a simple transformation, we can derive the equilibrium output-to-capital ratio, which remains constant at the steady state:

The equation can be further transformed into per worker form, which provides a more intuitive representation for understanding the steady-state equilibrium.

At the steady state, the saving/investment per worker in the economy (sy) are just sufficient for:

• deepening capital stock at the rate of g
• replacing the depreciated plant and equipment
• providing capital for new workers

A higher saving rate results in a higher steady-state level of capital per worker and output per worker. However, the long-term growth rate of output per worker is unchanged.

A higher depreciation rate reduces the steady-state level of capital per worker and output per worker due to additional investment is needed to replace depreciated capital, leaving less for capital deepening.

A higher population growth rate reduces the steady-state level of capital per worker and output per worker due to labour force requires more investment to maintain the same level of capital per worker.

A higher technology growth rate leads to increased growth rate in output per worker over time.

• Coding towards CFA