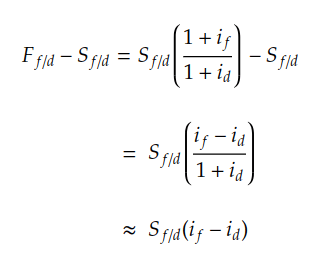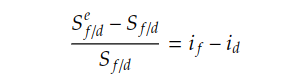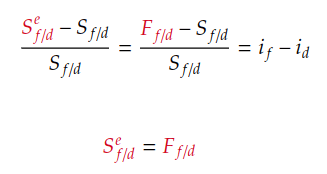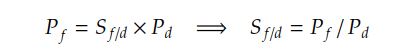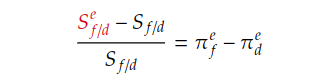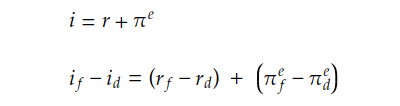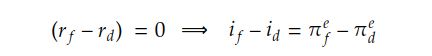This is the first code-less blog post in my Coding Towards CFA series. I’ve included this topic because of the importance of International Parity Conditions, which form the theoretical foundation of forex trading. These conditions are essential for gaining a deep understanding of equilibrium pricing, enabling investors to navigate the FX market more effectively. One of the main challenges in FX investing is the prevalence of short-term noise. International parity conditions provide a structured framework for understanding how exchange rates are determined in the long term, making them a critical tool for analysing the underlying forces driving exchange rate changes.

Here are the five key international parity conditions covered in the CFA curriculum, including:

• Covered Interest Rate Parity
• Uncovered Interest Rate Parity
• Forward Rate Parity
• Purchasing Power Parity
• International Fisher Parity

In this blog post, I’ll distill the key insights I’ve gained from studying these conditions. Unlike the lengthy explanations often found in other literature, my aim is to present the most important takeaways in a clear and concise manner.

Interest Rate Parity

The Interest Rate Parity (IRP) conditions construct a theoretical link between exchange rates and interest rates. According to IRP:

• The forward exchange rate, F(f/d), of a currency with lower interest rates will rise relative to the spot rate
• The forward exchange rate, F(f/d), of a currency with higher interest rates will fall relative to the spot rate

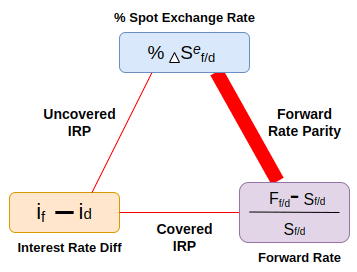
Therefore, differences in interest rates between two countries are offset by expected movements in their exchange rates, ultimately leading to a state of equilibrium in the foreign exchange market.

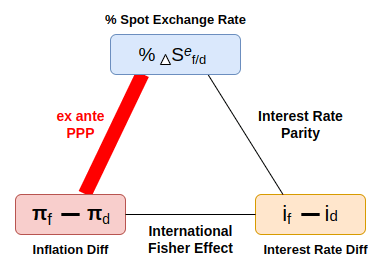
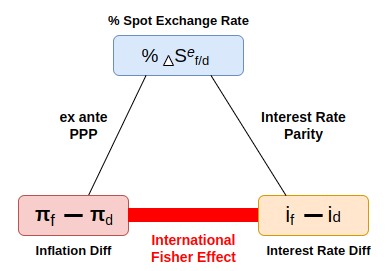
Interest Rate Parity involves the relationship between changes in the spot exchange rate, the difference between domestic and foreign interest rates, and the forward rate. This relationship can be illustrated in the following triangle.

Covered Interest Rate Parity

Covered interest rate parity is a no-arbitrage condition in which investors use forward contracts to eliminate foreign exchange risk. This ensures that the returns on investments in domestic and foreign markets are equal. According to covered interest rate parity, the market will reach a forward exchange rate that offsets the interest rate difference between the two currencies involved.

Therefore, the difference between the forward rate and spot rate is determined by the difference between the nominal interest rates.

Uncovered Interest Rate Parity

For covered interest rate parity, the forward exchange rate is locked in through a forward contract to eliminate exchange rate risk. In contrast, the uncovered interest rate parity does not involve hedging, and has no locked in forward exchange rate to assure the interest rate parity. Instead, uncovered interest rate parity relies on the expected future spot rate (E[St]), and the change from current spot rate to the future spot rate is being driven by the difference between the interest rates of the involved currencies.

Compared to the covered interest rate parity, the uncovered interest rate parity is less reliable, which relies on the uncertain expected future spot rate and leave investors exposed to exchange rate risk. Under the uncovered interest rate parity, the domestic currency is expected to appreciate (depreciate) by approximately i(f) – i(d) when the interest rate difference is positive(negative).

Forward Rate Parity

When covered interest rate parity holds, the following equation holds:

When uncovered interest rate parity holds, the following equation holds:

Then, the transformation of the equation leads us to the conclusion that the forward exchange rate is equal to the expected future exchange rate, i.e., the forward exchange rate is an unbiased forecast of the future spot exchange rate if both covered and uncovered interest rate parities hold.

Purchasing Power Parity

According to the law of one price, same goods should trade at the same price across countries. Therefore, the foreign price of good should be equal to the domestic price of the same good adjusted with the exchange rate. So, the exchange rate should be determined by the ratio of the foreign and domestic broad price indexes. This is the absolute version of PPP.

The absolute version of PPP is highly unlikely to hold in the real world as the weights of the various goods in the two countries are hardly same.

The relative version of PPP is more applicable in the real world, where changes in exchange rates are determined by the difference between foreign and domestic inflation rates. In other words, exchange rates adjust to reflect differences in inflation rates between two countries. While the relative version of PPP focuses on actual changes in exchange rates driven by actual differences in national inflation rates, the ex ante version of PPP is more useful for understanding the relationship between expected exchange rates and expected future inflation rates.

International Fisher Effect

The nominal interest rate can be broken down into two components: the real interest rate (r) and the expected inflation rate. When comparing nominal interest rates between two countries, the difference can be calculated as the sum of the difference in real interest rates and the difference in inflation rates, as shown in the following equations.

According to the second equation shown above, if real interest rate parity holds, the real interest rate will converge to the same level across different markets. Therefore, we can conclude that the difference in nominal interest rates is equal to the difference in inflation rates, which is the essence of the International Fisher Effect.

• Coding towards CFA