The valuation and analysis of bonds with embedded options is the most focused topic discussed in the CFA Level 2 Fixed Income curriculum. These types of bonds, such as callable and puttable bonds, introduce an additional layer of complexity due to the optionality features embedded within the instrument. In this blog post, I will discuss the characteristics of callable and puttable bonds and walk through the code for pricing them with support from the QuantLib library.

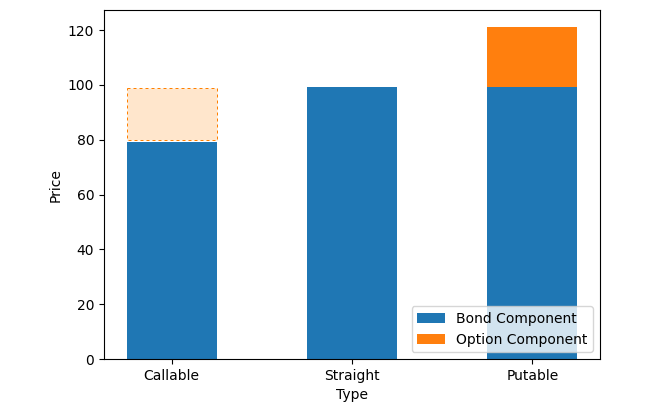
A callable bond grants the issuer the right, but not the obligation, to redeem or “call” the bond before its maturity date at a predetermined price, known as the call price. This type of bonds offer flexibility to the issuer but create additional risks for investors, which allows the issuer to refinance the debt at a lower cost in a interest rate declining environment. As a result, callable bonds tend to offer higher yields to compensate investors for the possibility of early redemption. In the other words, a callable bond’s price is typically lower than that of an equivalent straight bond.

The price difference between a callable bond and its equivalent straight bond reflects the value of the embedded call option:

Call option = Straight bond – Callable bond

In other words, the value of a callable bond is equivalent to the value of a straight bond minus the value of the issuer’s call option.

Callable bond = Straight bond – (Issuer) call option

A putable bond gives the bondholder the right, but not the obligation, to sell the bond back to the issuer before its maturity date at a predetermined price, known as the put price. This types of bonds benefit the bondholder when interest rates rise, as they can sell the bond back and reinvest at higher rates.

The price difference between a putable bond and its equivalent straight bond reflects the value of the embedded put option:

Put option = Putable bond – Straight bond

Therefore, the value of a putable bond is equivalent to the value of a straight bond plus the value of the investor’s put option.

Putable bond = Straight bond + (Investor) put bond

Pricing Callable and Putable Bonds

The CFA Level 2 Fixed Income curriculum dedicates considerable attention to the pricing of callable and putable bonds using binomial interest rate trees. These methods are essential for understanding how embedded options affect the bond’s price. However, in practice, the tedious manual calculations required for these processes can be time-consuming and error-prone. Fortunately, in the real world, we can leverage ready-to-use pricing libraries, such as QuantLib, which simplify the process and allow for accurate and efficient pricing. In this section, I will walk through the steps for pricing callable and putable bonds using QuantLib.

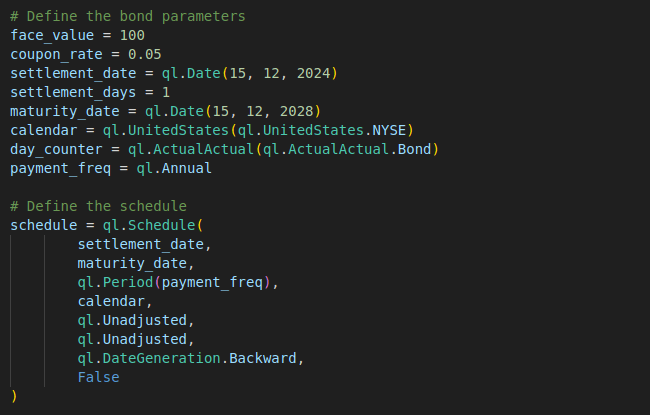
First, we define the general features and the cash flow schedule of a bond.

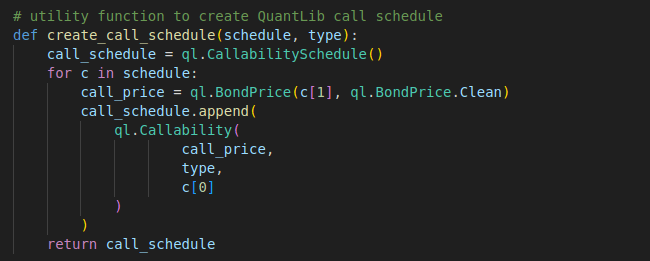
Second, we need to model the callability schedule of the bond in terms of its callable dates and call prices.

The QuantLib Callability object is shared for both callable type and putable type. We define the create_call_schedule function to create the CallabilitySchedule instance based on the defined callability schedule and the specified bond type, call or put.

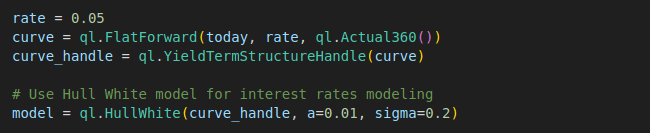
Next, we define the yield term structure and the interest rates model for simulating the interest rate paths for pricing. Here, we use the Hull White model, a QuantLib built-in model, which is one of the most widely used short-term interest rate models for pricing financial instruments. This model captures the dynamics of interest rates based on the assumption that interest rates will revert to a long-term mean over time.

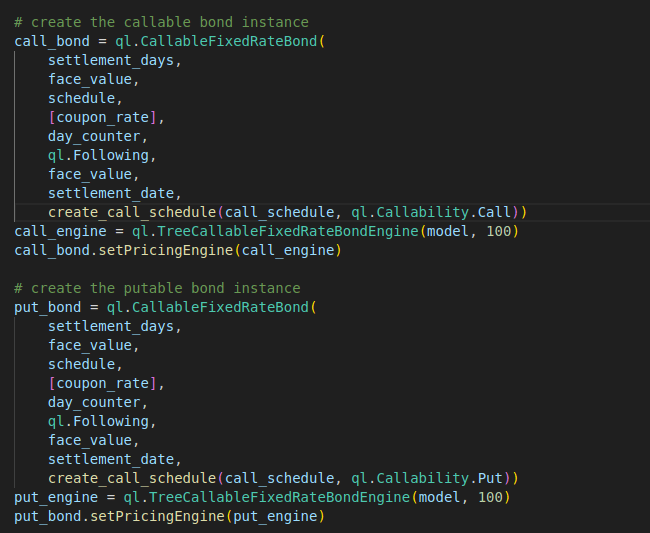
With the bond features, callability schedule and interest rate model in place, we can create the QuantLib CallableFixedRateBond instance, which encapsulates the common functions for valuing callable and putable bonds, such as calculating OAS, effective duration and convexity, and implied volatility.

The code for creating a callable bond and a putable bond is very similar. The only difference is the bond type specified for creating the callabiblity schedule, ql.Callability.Call or ql.Callability.Put.

For the pricing engine, we create a TreeCallableFixedRateBondEngine instance using the Hull-White interest rate model we defined earlier. In short, this pricing engine will simulate interest rate movements using a tree-based method and calculate the bond’s price while taking into account the embedded call option.

With the created callable and putable bond instances, we can call the NPV() method to trigger the calculation of the bond values and calculate the embedded option prices by comparing the callable/putable bond price with the straight bond price. The full version of code can be found below.

Full Code – Python

import QuantLib as ql
import numpy as np
import matplotlib.pyplot as plt

# utility function to create QuantLib call schedule
def create_call_schedule(schedule, type):
    call_schedule = ql.CallabilitySchedule()
    for c in schedule:
        call_price = ql.BondPrice(c[1], ql.BondPrice.Clean)
        call_schedule.append(
            ql.Callability(
                    call_price,
                    type,
                    c[0]
            )
        )
    return call_schedule

# utility function to plot stacked bar chart
def draw_stacked_bar_chart(x, y1, y2, x_label, y_label, y1_label, y2_label, width):
    fig, ax = plt.subplots()
    ax.bar(x, y1, label=y1_label, width=width)
    ax.bar(x, y2, bottom=y1, label=y2_label, width=width)  
    ax.set_xlabel(x_label)
    ax.set_ylabel(y_label)
    ax.set_title('')
    ax.legend(loc='lower right')
    plt.show()

# Set evaluation date for QuantLib
today = ql.Date(23, 12, 2024)
ql.Settings.instance().evaluationDate = today

# Define the bond parameters
face_value = 100 
coupon_rate = 0.05
settlement_date = ql.Date(15, 12, 2024)
settlement_days = 1
maturity_date = ql.Date(15, 12, 2028)
calendar = ql.UnitedStates(ql.UnitedStates.NYSE)
day_counter = ql.ActualActual(ql.ActualActual.Bond)
payment_freq = ql.Annual

# Define the schedule
schedule = ql.Schedule(
        settlement_date, 
        maturity_date, 
        ql.Period(payment_freq), 
        calendar, 
        ql.Unadjusted, 
        ql.Unadjusted, 
        ql.DateGeneration.Backward, 
        False
)

# Define the callability schedule
call_schedule=[
    (ql.Date(15, 12, 2026), 100),
    (ql.Date(15, 12, 2027), 100),
]

rate = 0.05
curve = ql.FlatForward(today, rate, ql.Actual360())
curve_handle = ql.YieldTermStructureHandle(curve)

# Use Hull White model for interest rates modeling
model = ql.HullWhite(curve_handle, a=0.01, sigma=0.2)

# create the callable bond instance
call_bond = ql.CallableFixedRateBond(
    settlement_days, 
    face_value,
    schedule, 
    [coupon_rate],
    day_counter,
    ql.Following, 
    face_value, 
    settlement_date,
    create_call_schedule(call_schedule, ql.Callability.Call))
call_engine = ql.TreeCallableFixedRateBondEngine(model, 100)
call_bond.setPricingEngine(call_engine)

# create the putable bond instance
put_bond = ql.CallableFixedRateBond(
    settlement_days, 
    face_value,
    schedule, 
    [coupon_rate],
    day_counter,
    ql.Following, 
    face_value, 
    settlement_date,
    create_call_schedule(call_schedule, ql.Callability.Put))
put_engine = ql.TreeCallableFixedRateBondEngine(model, 100)
put_bond.setPricingEngine(put_engine)

# create the straight bond instance
straight_bond = ql.FixedRateBond(
    settlement_days, 
    face_value, 
    schedule, 
    [coupon_rate], 
    day_counter)
straight_engine = ql.DiscountingBondEngine(curve_handle)
straight_bond.setPricingEngine(straight_engine)

callable_price = call_bond.NPV()
straight_price = straight_bond.NPV()
putable_price = put_bond.NPV()

X = ["Callable", "Straight", "Putable"]
Y1 = [callable_price, straight_price, straight_price]
Y2 = [0, 0, putable_price-straight_price]
draw_stacked_bar_chart(X, Y1 , Y2, 'Type'
                       , 'Price', 'Bond Component', 'Option Component', 0.5)

• Coding towards CFA
• QuantLib