Delta hedging is an options trading strategy used to maintain a delta neutral position by ensuring that the overall delta of a portfolio is zero, so that the price fluctuations of the underlying asset do not significantly impact the position’s value. Dynamic delta hedging involves continuously adjusting the hedging position to account for changes in the underlying asset’s price.
A common application of dynamic delta hedging is in risk management for market makers in options contracts. For instance, a market maker might sell call options on a stock, exposing them to the risk of the stock’s price rising. To offset this risk, they can implement dynamic delta hedging by buying the underlying stock for balancing the changes in the option’s value as the stock price moves. This hedging position is constantly adjusted as the stock’s price fluctuates.
In this blog post, I will explore the implementation of dynamic delta hedging using DolphinDB’s stream processing framework for an assumed use case: a market maker holds a short position in a call option on x shares of stock. To implement dynamic delta hedging, we will calculate the delta of the short call option position and then determine the number of shares of the underlying stock needed to go long, thereby neutralising the delta exposure. I will break down the implementation into the following four steps:
- Step 1 – Create the required DolphinDB tables
- Step 2 – Simulate the stock price movements
- Step 3 – Create stream processing for dynamic delta hedging
- Step 4 – Build real-time dashboard using DolphinDB
Create the required DolphinDB tables
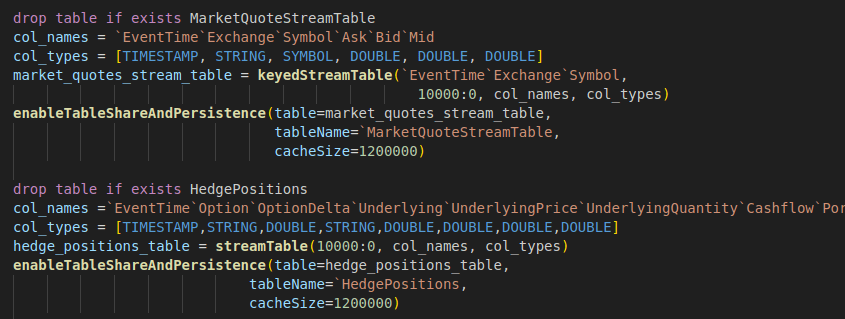
For this demo, we use two stream tables: the first, “MarketQuoteStreamTable”, to receive real-time price quotes of the underlying stock for the option contract, and the second, “HedgePositions”, to output the calculated hedge positions.
Simulate the stock price movements
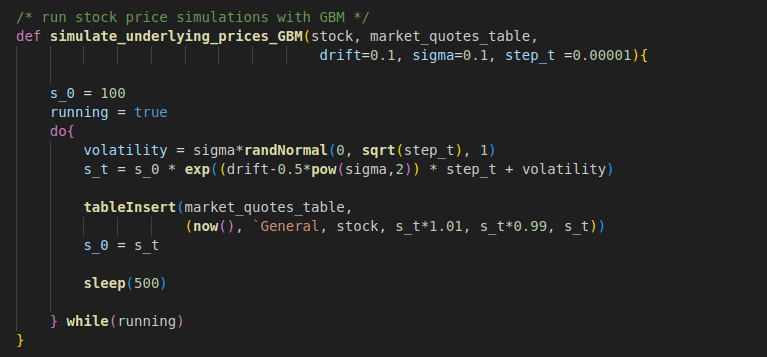
We will simulate the real-time price quotes of the underlying stock for the option contract in GBM motion. Please refer to Coding towards CFA (9) – From Binomial Model to BSM for an explanation of why and how we use GBM. The simulated stock prices will be ingested into the MarketQuoteStreamTable.
Create stream processing for dynamic delta hedging
The MarketQuoteStreamTable stream table is subscribed to, and the new underlying stock price quotes are processed by the handler, daynamic_delta_hedging.
The delta hedging logic is relatively straightforward:
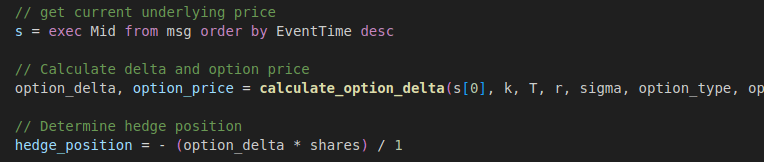
- Calculate the option delta and price are using the latest underlying stock price.
- Calculate the total delta of the option position, i.e., option delta * option shares
- Calculate the hedge position, i.e., the shares of stock to neutralise the delta. Since the delta of the stock is always 1, the hedge position is calculated as: – (option_delta * shares) / 1
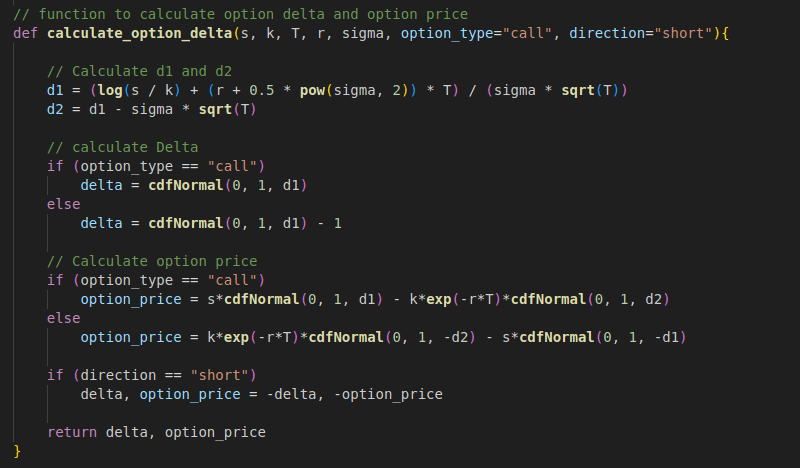
The function for calculating option delta and price using BSM.
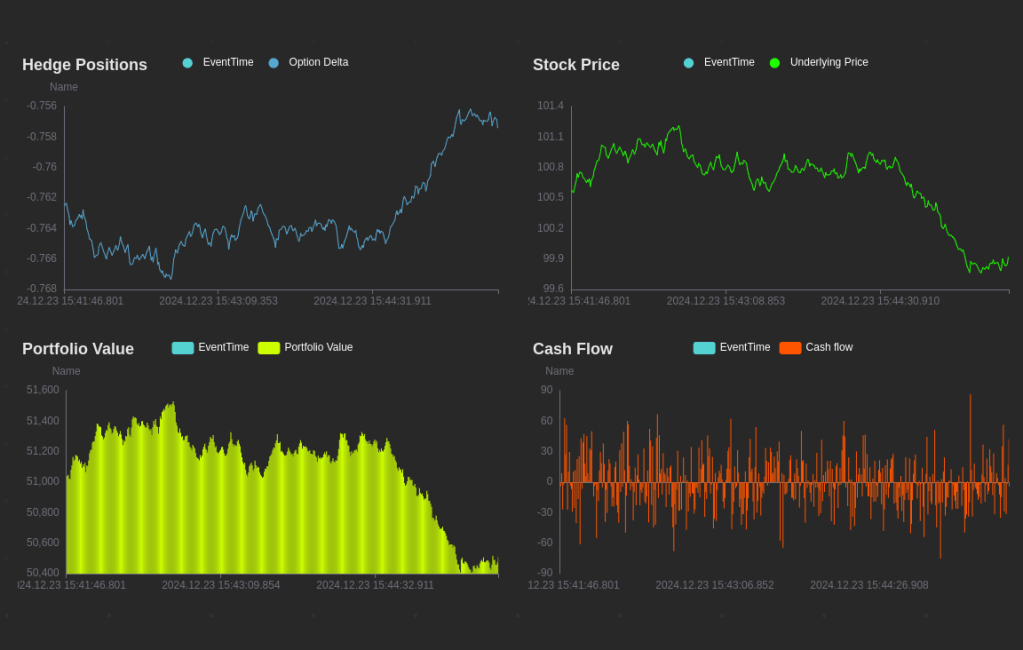
Once the new hedge position is calculated based on the latest market data, we can use this information to adjust the portfolio and neutralise the delta. We can determine the number of stock shares to buy or sell in order to neutralise the delta. Additionally, we can calculate the updated total portfolio value.
Build real-time dashboard using DolphinDB
All the new results will be output to the HedgePositions stream table for downstream use, such as generating real-time charts using DolphinDB’s built-in dashboard feature.
Full Code – DolphinDB
Create Tables
drop table if exists MarketQuoteStreamTable
col_names = `EventTime`Exchange`Symbol`Ask`Bid`Mid
col_types = [TIMESTAMP, STRING, SYMBOL, DOUBLE, DOUBLE, DOUBLE]
market_quotes_stream_table = keyedStreamTable(`EventTime`Exchange`Symbol,
10000:0, col_names, col_types)
enableTableShareAndPersistence(table=market_quotes_stream_table,
tableName=`MarketQuoteStreamTable,
cacheSize=1200000)
drop table if exists HedgePositions
col_names =`EventTime`Option`OptionDelta`Underlying`UnderlyingPrice`UnderlyingQuantity`Cashflow`PortfolioValue
col_types = [TIMESTAMP,STRING,DOUBLE,STRING,DOUBLE,DOUBLE,DOUBLE,DOUBLE]
hedge_positions_table = streamTable(10000:0, col_names, col_types)
enableTableShareAndPersistence(table=hedge_positions_table,
tableName=`HedgePositions,
cacheSize=1200000)
Stock Price Simulations
def simulate_underlying_prices_GBM(stock, market_quotes_table, drift=0.1, sigma=0.1, step_t =0.00001){
s_0 = 100
running = true
do{
s_t = s_0 * exp((drift-0.5*pow(sigma,2)) * step_t + sigma*randNormal(0, sqrt(step_t), 1))
tableInsert(market_quotes_table, (now(), `General, stock, s_t*1.01, s_t*0.99, s_t))
s_0 = s_t
sleep(500)
} while(running)
}
simulate_underlying_prices_GBM("Stock_1", MarketQuoteStreamTable)
Dynamic Delta Hedging
// function to calculate option delta and option price
def calculate_option_delta(s, k, T, r, sigma, option_type="call", direction="short"){
// Calculate d1 and d2
d1 = (log(s / k) + (r + 0.5 * pow(sigma, 2)) * T) / (sigma * sqrt(T))
d2 = d1 - sigma * sqrt(T)
// calculate Delta
if (option_type == "call")
delta = cdfNormal(0, 1, d1)
else
delta = cdfNormal(0, 1, d1) - 1
// Calculate option price
if (option_type == "call")
option_price = s*cdfNormal(0, 1, d1) - k*exp(-r*T)*cdfNormal(0, 1, d2)
else
option_price = k*exp(-r*T)*cdfNormal(0, 1, -d2) - s*cdfNormal(0, 1, -d1)
if (direction == "short")
delta, option_price = -delta, -option_price
return delta, option_price
}
// Dynamic delta hedging simulation
def dynamic_delta_hedging(k, r, sigma, expiration_date, shares, option_type, option_direction, msg){
// Calculate option period in year unit
T = (timestamp(expiration_date) - now()) / (1000*60*60*24*365)
// get current underlying price
s = exec Mid from msg order by EventTime desc
// Calculate delta and option price
option_delta, option_price = calculate_option_delta(s[0], k, T, r, sigma, option_type, option_direction)
// Determine hedge position
hedge_position = - (option_delta * shares) / 1
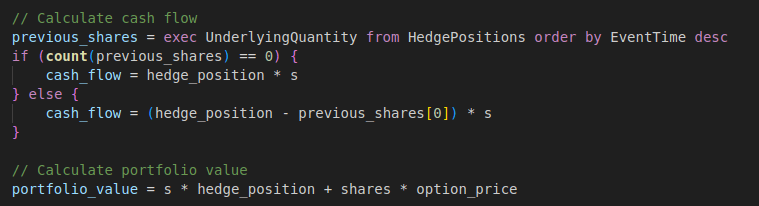
// Calculate cash flow
previous_shares = exec UnderlyingQuantity from HedgePositions order by EventTime desc
if (count(previous_shares) == 0) {
cash_flow = hedge_position * s
} else {
cash_flow = (hedge_position - previous_shares[0]) * s
}
// Calculate portfolio value
portfolio_value = s * hedge_position + shares * option_price
// Output to hedge positions stream table
insert into HedgePositions
values(now(), `Stock_1_Call, option_delta, `Stock_1, s, hedge_position, cash_flow, portfolio_value)
}
k, r, sigma, type, direction, expiration_date, shares = 100, 0.05, 0.2, "call", "short", 2025.03.15, 1000
if (`MarketQuoteStreamTable in getStreamingStat()['pubTables']['tableName']){
unsubscribeTable(tableName=`MarketQuoteStreamTable, actionName="delta_hedge")
}
subscribeTable(tableName=`MarketQuoteStreamTable,
actionName="delta_hedge",
msgAsTable=true,
handler=dynamic_delta_hedging{k, r, sigma, expiration_date, shares, type, direction})


Hi, your blog is great.
Thank you very much.