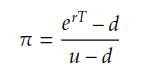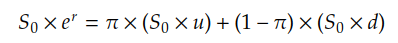In this blog series, I will aim to code the formulas and model algorithms covered in the CFA Level 2 program using Python and DolphinDB. Each topic will begin with a brief explanation of the formulas or algorithms, followed by their implementations in Python and DolphinDB.

From this blog post, we start our journey to explore how options are valued and the factors influencing their prices. We begin by introducing the binomial tree model, one of the most fundamental approach to option valuation. This method models the potential future price movements of an underlying asset, assuming that the price can either move up or down in a discrete-time, step-by-step process.

In this blog post, we begin with the simplest form of the binomial tree model: the one-period tree, which assumes there are only two possible future prices—one up and one down. While this assumption may seem unrealistic and the valuation may not have much real-world applicability, it serves as a great starting point for understanding the mechanism of how the binomial tree works in option pricing.

Steps of Options Valuation with Binomial Model

The valuation of options using the Binomial model can be broken down into the following steps. These steps apply not only to the one-period binomial model but also to the multi-period binomial model.

• Calculate the up and down factors
• Calculate the up and down probabilities
• Calculate underlying prices at expiration
• Calculate the option payoffs at expiration
• Backward induction of option value at the initiation

Here is an implementation of each step for the one-period binomial model.

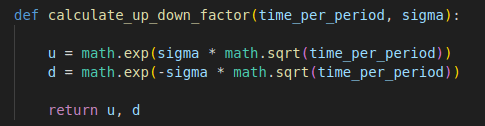
Step 1 – Calculate the up and down factors

We need first to determine the up factor and the down factor, where the up factor represents the price of the underlying asset will increase in one period, and the down factor represents the price descrease path.

The formula assumes that price movements follow a geometric Brownian motion (GBM) model, where the price of the asset changes randomly but with a predictable distribution of possible changes. The GBM is not the focus of this blog post, but I plan to write a dedicated blog post to simulate the GBM model. The up and down factors are typically determined using volatility and the time step, where volatility (sigma) indicates the degree of variation in the asset’s price.

Here is the python function for implementing these formulas.

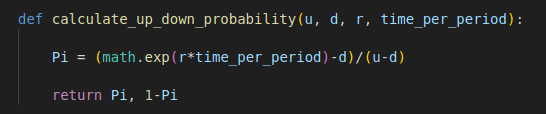
Step 2 – Calculate the up and down probabilities

The probability of the price moving up can be calculated as:

which is derived from the formula for calculating future asset price.

Here is the Python implementation.

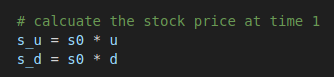
Step 3 – Calculate underlying prices at expiration

For one-period binomial model, only one step for calculating the final underlying price expiration as:

Step 4 – Calculate the option payoffs at expiration

Based on the calculated underlying prices at expiration, we can work out the option payoffs for both price up and price down scenarios.

Step 5 – Backward induction of option value at the initiation

With the option payoffs and the probabilities of price up and down available, we can determine the option’s value at initiation by calculating the present value of the option’s payoffs at expiration.

Full Code – Python

import math

def calculate_up_down_factor(time_per_period, sigma):

    u = math.exp(sigma * math.sqrt(time_per_period))
    d = math.exp(-sigma * math.sqrt(time_per_period))

    return u, d

def calculate_up_down_probability(u, d, r, time_per_period):
    
    Pi = (math.exp(r*time_per_period)-d)/(u-d)

    return Pi, 1-Pi


def binomial_tree_1_period(s0, k, T, r, sigma, option_type="call"):

    number_of_periods = 1
    time_per_period = T/number_of_periods
    
    # Calculate the up and down factors
    u, d = calculate_up_down_factor(time_per_period, sigma)
    
    # Calculate the up and down probabilities
    Pi_up, Pi_down = calculate_up_down_probability(u, d, r, time_per_period)
    
    # Calculate underlying prices at expiration
    s_u = s0 * u
    s_d = s0 * d

    # Calculate the option payoffs at expiration
    if option_type == "call":
        c_u = max(s_u - k, 0) 
        c_d = max(s_d - k, 0) 
    else:
        c_u = max(k - s_u, 0)
        c_d = max(k - s_d, 0)

    # Backward induction of option value at the initiation
    option_price = (Pi_up*c_u+Pi_down*c_d)/math.exp(r*time_per_period)

    return option_price


s0 = 100  
k = 100
T = 1
r = 0.0515
sigma = 0.3

call_price = binomial_tree_1_period(s0, k, T, r, sigma, option_type="call")
print("the option price is: " + str(call_price))

put_price = binomial_tree_1_period(s0, k, T, r, sigma, option_type="put")
print("the option price is: " + str(put_price))

Full Code – DolphinDB

def calculate_up_down_factor(time_per_period, sigma){

    u = exp(sigma * sqrt(time_per_period))
    d = exp(-sigma * sqrt(time_per_period))

    return u, d
}

def calculate_up_down_probability(u, d, r, time_per_period){
    
    Pi = (exp(r*time_per_period)-d)/(u-d)

    return Pi, 1-Pi
}


def binomial_tree_1_period(s0, k, T, r, sigma, option_type="call") {

    number_of_periods = 1
    time_per_period = T/number_of_periods
    
    // Calculate the up and down factors
    u, d = calculate_up_down_factor(time_per_period, sigma)
    
    // calculate the up and down probabilities
    Pi_up, Pi_down = calculate_up_down_probability(u, d, r, time_per_period)
    
    // Calculate underlying prices at expiration
    s_u = s0 * u
    s_d = s0 * d

    // Calculate the option payoffs at expiration
    if (option_type == "call") {
        c_u = max(s_u - k, 0) 
        c_d = max(s_d - k, 0) 
    } else{
        c_u = max(k - s_u, 0)
        c_d = max(k - s_d, 0)
    }

    // Backward induction of option value at the initiation
    option_price = (Pi_up*c_u+Pi_down*c_d)/exp(r*time_per_period)

    return option_price

}

s0 = 100  
k = 100
T = 1
r = 0.0515
sigma = 0.3

call_price = binomial_tree_1_period(s0, k, T, r, sigma, option_type="call")
print("the option price is: " + call_price)

put_price = binomial_tree_1_period(s0, k, T, r, sigma, option_type="put")
print("the option price is: " + put_price)

• Coding towards CFA