In this blog series, I will aim to code the formulas and model algorithms covered in the CFA Level 2 program using Python and DolphinDB. Each topic will begin with a brief explanation of the formulas or algorithms, followed by their implementations in Python and DolphinDB.
A currency swap is a financial agreement where two parties exchange principal amounts and interest payments in different currencies. This arrangement enables each party to obtain financing in a foreign currency indirectly, without needing to borrow in that currency directly. A currency swap contract spans the following stages:
- Principal Exchange (time 0) – the two parties exchange the notional amount of principal in their respective currencies.
- Interest Payments (time t) – interest payments are made periodically, where each party pays the interest of the currency they received at the agreed rate.
- Terminal Principal Exchange (time T) – the principal amounts are re-exchanged.
This blog post will explore the pricing and valuing currency swap contracts, with focus on the fixed-to-fixed currency swap.
Currency Swap Contract Pricing
Pricing a fixed-to-fixed currency swap involves determining the fixed interest rate for each currency leg such that the present values of the payments on both sides are equal. This ensures the swap has a net value of zero at inception, reflecting fair pricing for both parties.
For a currency swap contract, at its initiation, the principal notional amount of one currency (NA_a) is given. As the market spot exchange rate (S0) is available, the principal notional amount of the counterparty currency (NA_b) can also be calculated as:
NA_b = S0 X NA_a
With the known NA_a and NA_b, we can calculate the present values of the future payments for each swap leg as:
- V_a = sum(PV(NA_a x Fixed_Rate_a)) + PV(NA_a)
- V_b = sum(PV(NA_b x Fixed_Rate_b)) + PV(NA_b)
Now, the pricing of the swap contract involves determining the Fixed_Rate_a and the Fixed_Rate_b such that the V_b = S0 x V_a.
Below is a Python implementation for the logic described, which uses the fsolve function from the scipy.optimize library to solve the fixed_rate_a and the fixed_rate_b.
Currency Swap Contract Valuation
The valuation of a currency swap contract simply involves comparing the difference in the present values of the future payments of both legs.
Full Code – Python
import numpy as np
from scipy.optimize import fsolve
def calculate_discount_factors(days_to_maturity, spot_rates):
return np.array([1/(1+r*(d/360))
for r, d in zip(spot_rates, days_to_maturity)])
def calculate_currency_swap_price(days_to_maturity, ccy_1_rates, ccy_1_na,
ccy_2_rates, exchange_rate, payments_per_year):
ccy_1_discount_factors = calculate_discount_factors(days_to_maturity, ccy_1_rates)
ccy_2_discount_factors = calculate_discount_factors(days_to_maturity, ccy_2_rates)
ccy_2_na = ccy_1_na * exchange_rate
def calculate_currency_swap_price(days_to_maturity, ccy_1_rates, ccy_1_na, ccy_2_rates, exchange_rate, payments_per_year):
ccy_1_discount_factors = calculate_discount_factors(days_to_maturity, ccy_1_rates)
ccy_2_discount_factors = calculate_discount_factors(days_to_maturity, ccy_2_rates)
ccy_2_na = ccy_1_na * exchange_rate
def solve_currency_swap_fixed_rates(guess):
ccy_1_fixed_rate, ccy_2_fixed_rate = guess
ccy1_payments_pv = np.sum(
[ccy_1_na * ccy_1_fixed_rate / payments_per_year * df
for df in ccy_1_discount_factors]
) + ccy_1_na * ccy_1_discount_factors[-1]
ccy2_payments_pv = np.sum(
[ccy_2_na * ccy_2_fixed_rate / payments_per_year * df
for df in ccy_2_discount_factors]
) + ccy_2_na * ccy_2_discount_factors[-1]
return ccy1_payments_pv * exchange_rate - ccy2_payments_pv, 0
initial_guess = [0.03, 0.02]
fixed_rates = fsolve(solve_currency_swap_fixed_rates, initial_guess)
return fixed_rates, ccy_2_na
initial_guess = [0.03, 0.02]
fixed_rates = fsolve(solve_currency_swap_fixed_rates, initial_guess)
return fixed_rates, ccy_2_na
days_to_maturity = [90, 180, 270, 360]
ccy_1_rates = [0.025, 0.026, 0.027, 0.028]
ccy_2_rates = [0.001, 0.0015, 0.002, 0.0025]
ccy_1_na = 100000000
exchange_rate = 0.8772
payments_per_year = 4
print(calculate_currency_swap_price(days_to_maturity, ccy_1_rates, ccy_1_na,
ccy_2_rates, exchange_rate, payments_per_year))
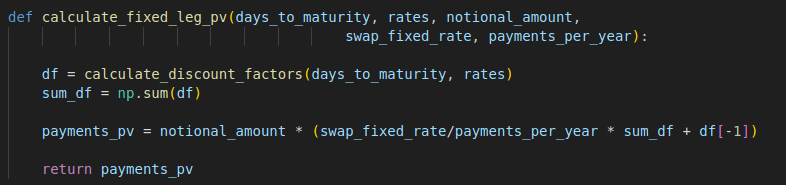
def calculate_fixed_leg_pv(days_to_maturity, rates, notional_amount, swap_fixed_rate, payments_per_year):
df = calculate_discount_factors(days_to_maturity, rates)
sum_df = np.sum(df)
payments_pv = notional_amount * (swap_fixed_rate/payments_per_year * sum_df + df[-1])
return payments_pv
def calculate_currency_swap_value(days_to_maturity, ccy_1_rates, ccy_1_na, ccy_1_swap_fixed_rate,
ccy_2_rates, ccy_2_na, ccy_2_swap_fixed_rate, exchange_rate, payments_per_year):
ccy1_payments_pv = calculate_fixed_leg_pv(days_to_maturity, ccy_1_rates, ccy_1_na,
ccy_1_swap_fixed_rate, payments_per_year)
ccy2_payments_pv = calculate_fixed_leg_pv(days_to_maturity, ccy_2_rates, ccy_2_na,
ccy_2_swap_fixed_rate, payments_per_year)
return ccy1_payments_pv - exchange_rate* ccy2_payments_pv
days_to_maturity = [30, 120, 210, 300]
ccy_1_rates = [0.02, 0.019, 0.018, 0.017]
ccy_2_rates = [0.005, 0.004, 0.003, 0.002]
ccy_1_swap_fixed_rate = 0.027695
ccy_2_swap_fixed_rate = 0.002497
ccy_1_na = 100000000
ccy_2_na = 87719298
exchange_rate = 1.13
payments_per_year = 4
print(calculate_currency_swap_value(days_to_maturity,
ccy_1_rates, ccy_1_na,
ccy_1_swap_fixed_rate,
ccy_2_rates, ccy_2_na,
ccy_2_swap_fixed_rate,
exchange_rate, payments_per_year))
Full Code – DolphinDB
def calculate_fixed_leg_pv(days_to_maturity, rates, notional_amount, swap_fixed_rate, payments_per_year){
df = calculate_discount_factors(days_to_maturity, rates)
sum_df = sum(df)
payments_pv = notional_amount * (swap_fixed_rate/payments_per_year * sum_df + last(df))
return payments_pv
}
def calculate_currency_swap_value(days_to_maturity, ccy_1_rates, ccy_1_na, ccy_1_swap_fixed_rate,
ccy_2_rates, ccy_2_na, ccy_2_swap_fixed_rate,
exchange_rate, payments_per_year){
ccy1_payments_pv = calculate_fixed_leg_pv(days_to_maturity, ccy_1_rates, ccy_1_na, ccy_1_swap_fixed_rate, payments_per_year)
ccy2_payments_pv = calculate_fixed_leg_pv(days_to_maturity, ccy_2_rates, ccy_2_na, ccy_2_swap_fixed_rate, payments_per_year)
return ccy1_payments_pv - exchange_rate* ccy2_payments_pv
}
days_to_maturity = [30, 120, 210, 300]
ccy_1_rates = [0.02, 0.019, 0.018, 0.017]
ccy_2_rates = [0.005, 0.004, 0.003, 0.002]
ccy_1_swap_fixed_rate = 0.027695
ccy_2_swap_fixed_rate = 0.002497
ccy_1_na = 100000000
ccy_2_na = 87719298
exchange_rate = 1.13
payments_per_year = 4
print(calculate_currency_swap_value(days_to_maturity,
ccy_1_rates,
ccy_1_na,
ccy_1_swap_fixed_rate,
ccy_2_rates,
ccy_2_na,
ccy_2_swap_fixed_rate,
exchange_rate, payments_per_year))