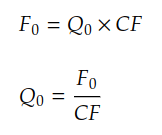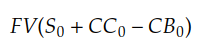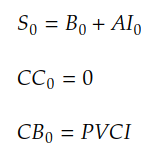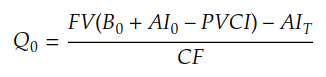In this blog series, I will aim to code the formulas and model algorithms covered in the CFA Level 2 program using Python and DolphinDB. Each topic will begin with a brief explanation of the formulas or algorithms, followed by their implementations in Python and DolphinDB.
Bond futures are financial contracts that obligate the buyer or seller to purchase or sell a bond at a predetermined price on a specified future date. They can be used for speculating on bond price changes or to hedge existing bond investments. Although not directly tied to interest rates, bond futures can also serve as a tool for trading or managing risks associated with interest rate fluctuations.
Bonds futures some unique characteristics that pricing of them needs account for.
Unique Characteristics of Bond Futures
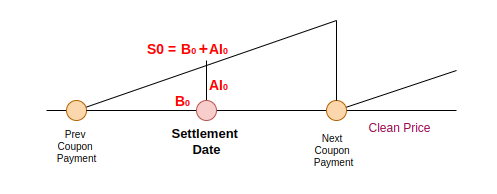
1) Clean Price vs Dirty Price
In some countries, the quoted bond price doesn’t include the interest that has built up since the last coupon payment. This is called the “clean price“, However, when buying or selling a bond, the deal must include the accrued interest, which is called the “dirty price“.
Accrued Interest = Accrual Period X Periodic Coupon Amount
- AI – accrued interest
- NAD – number of accrued days since last coupon payment
- NTD – total days of coupon payment period
- C – coupon amount
- n – coupon payments per year
2) Conversion Factor (CF)
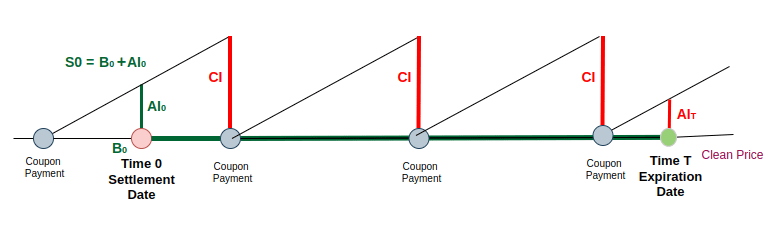
Bond futures contracts normally have a basket of bonds that can be delivered by the seller. These bonds can have different maturities and coupon rates, which results in different bond prices. To ensure all these bonds are treated fairly when delivered into the futures contract, a conversion factor is used, which adjusts the quoted futures price to match the value of the specific bond being delivered, in a formula like this:
Future Adjusted Price = Quoted Futures Price X CF
We can derive the formula to calculate the quoted futures price from the bond prices and conversion factor, which will be used for bond futures pricing.
3) Cheapest-to-Delivery (CTD) Bond
Since there is a basket of bonds that can be delivered for a specific bond futures contract, sellers typically select the cheapest to deliver (of course). The Cheapest-to-Delivery (CTD) bond is then normally considered in bond futures pricing, as it is the bond that will most likely to be delivered.
Pricing Bond Futures
Following the general forwards and futures pricing mechanism, the price of a bond future is the future value of the underlying bond, with all financing costs, carry costs, and carry benefits incorporated. This can be expressed with the following formula:
- FV – future value
- S(0) – spot price of the bond at time 0
- CC(0) – the carry costs value at time 0
- C B(0) – the carry benefits value at time 0
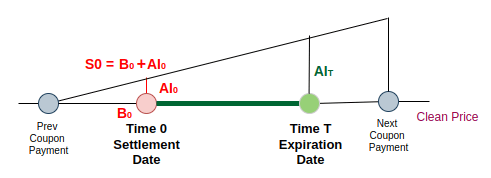
As discussed earlier, the spot price of the bond, S(0), is the dirty price, consists of the quoted price, B(0) and the accrued interest, AI(0):
For bonds, there are no carry costs to consider in bond futures pricing, so CC(0) = 0.
For bonds, the carry benefits are the coupon interest payments made during the contract period, PVCI.
Since the future value of the bond includes the accrued interest, AI(T), which is accumulated after the last coupon payment during the contract period, it needs to be removed when calculating the future price of the bond, F(0).
With the future price of the bond, we can now calculate the bond futures contract price using the conversion factor.
This is the code I wrote based on the calculation logic described above. * A full copy of the code can be found at the bottom of this blog post.
I have also created two functions for calculating the accrued interest (for AI(0) and AI(T)) and PVCI. The snapshot below shows the code for calculating the accrued interest.
Regarding the coupon interest, there are two situations. In the first situation, there is no coupon payment during the contract period, so the PVCI = 0.
The second situation is more complex, where one or more coupon payments occur during the contract period. These payments, which occur at different points in time, need to be discounted to calculate their present values.
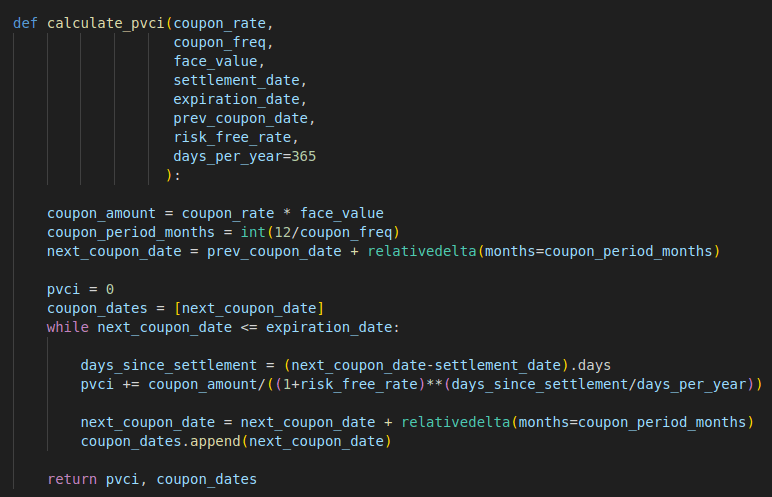
I created the “calculate_pvci” function to cover both situations.
Full Code – Python
from dateutil.relativedelta import relativedelta
from datetime import datetime
def calculate_accrued_interest(coupon_rate,
coupon_freq,
face_value,
start_date,
end_date,
days_per_year=365):
days_in_coupon_period = days_per_year/coupon_freq
days_since_prev_coupon_date = (end_date-start_date).days
coupon_amount = coupon_rate * face_value
accrued_interest = coupon_amount * (days_in_coupon_period
/days_since_prev_coupon_date
)
return accrued_interest
def calculate_pvci(coupon_rate,
coupon_freq,
face_value,
settlement_date,
expiration_date,
prev_coupon_date,
risk_free_rate,
days_per_year=365
):
coupon_amount = coupon_rate * face_value
coupon_period_months = int(12/coupon_freq)
next_coupon_date = prev_coupon_date + relativedelta(months=coupon_period_months)
pvci = 0
coupon_dates = [next_coupon_date]
while next_coupon_date <= expiration_date:
days_since_settlement = (next_coupon_date-settlement_date).days
pvci += coupon_amount/((1+risk_free_rate)**(days_since_settlement/days_per_year))
next_coupon_date = next_coupon_date + relativedelta(months=coupon_period_months)
coupon_dates.append(next_coupon_date)
return pvci, coupon_dates
def price_bond_future(current_bond_price, face_value, coupon_rate,coupon_freq,
settlement_date, expiration_date, prev_coupon_date, risk_free_rate,
conversion_factor,days_per_year=365):
#calculate AI(0)
accrued_interest_at_settlement = calculate_accrued_interest(coupon_rate, coupon_freq, face_value
,settlement_date, prev_coupon_date, days_per_year)
#calculate PVCI
pvci, coupon_dates = calculate_pvci(coupon_rate, coupon_freq, face_value, settlement_date
,expiration_date, prev_coupon_date, risk_free_rate, days_per_year)
#calculate AI(T)
accrued_interest_at_expiration = calculate_accrued_interest(coupon_rate, coupon_freq, face_value
,coupon_dates[-1], expiration_date, days_per_year)
#S(0) = B(0) + AI(0)
full_price = current_bond_price + accrued_interest_at_settlement
#FV(B(0)+AI(0)-PVCI)
contract_period = (expiration_date - settlement_date).days/days_per_year
future_value = (full_price - pvci)*((1+risk_free_rate)**contract_period)
#F(0) = FV(B(0)+AI(0)-PVCI) - AI(T)
adjusted_future_price = future_value - accrued_interest_at_expiration
#Q(0) = F(0)/CF
quoted_future_price = adjusted_future_price / conversion_factor
return quoted_future_price
current_bond_price = 108
face_value = 100
coupon_rate = 0.02
coupon_freq = 2
settlement_date = datetime(2024, 2, 15)
expiration_date = datetime(2024, 10, 15)
prev_coupon_date = datetime(2024, 1, 15)
risk_free_rate = 0.001
conversion_factor = 0.729535
quoted_bond_future_price = price_bond_future(
current_bond_price,
face_value,
coupon_rate,
coupon_freq,
settlement_date,
expiration_date,
prev_coupon_date,
risk_free_rate,
conversion_factor
)
print(f"The bond future price is: {quoted_bond_future_price:.2f}")
Full Code – DolphinDB
def calculate_accrued_interest(coupon_rate,
coupon_freq,
face_value,
start_date,
end_date,
days_per_year=365){
days_in_coupon_period = days_per_year/coupon_freq
days_since_prev_coupon_date = end_date-start_date
coupon_amount = coupon_rate * face_value
accrued_interest = coupon_amount * (days_in_coupon_period/days_since_prev_coupon_date)
return accrued_interest
}
def calculate_pvci(coupon_rate,
coupon_freq,
face_value,
settlement_date,
expiration_date,
prev_coupon_date,
risk_free_rate,
days_per_year=365){
coupon_amount = coupon_rate * face_value
coupon_period_months = int(12/coupon_freq)
next_coupon_date = temporalAdd(prev_coupon_date, coupon_period_months, "M")
pvci = 0
coupon_dates = array(date)
coupon_dates.append!(next_coupon_date)
do {
if (next_coupon_date > expiration_date) {
break
}
else {
days_since_settlement = next_coupon_date-settlement_date
pvci += coupon_amount/pow((1+risk_free_rate), (days_since_settlement/days_per_year))
next_coupon_date = temporalAdd(next_coupon_date, coupon_period_months, "M")
coupon_dates.append!(next_coupon_date)
}
}
while (next_coupon_date <= expiration_date);
return pvci, coupon_dates
}
def price_bond_future(current_bond_price,
face_value,
coupon_rate,
coupon_freq,
settlement_date,
expiration_date,
prev_coupon_date,
risk_free_rate,
conversion_factor,
days_per_year=365){
//calculate AI(0)
accrued_interest_at_settlement = calculate_accrued_interest(coupon_rate, coupon_freq, face_value, settlement_date, prev_coupon_date, days_per_year)
//calculate PVCI
pvci, coupon_dates = calculate_pvci(coupon_rate, coupon_freq, face_value, settlement_date
,expiration_date, prev_coupon_date, risk_free_rate, days_per_year)
//calculate AI(T)
accrued_interest_at_expiration = calculate_accrued_interest(coupon_rate, coupon_freq, face_value
,last(coupon_dates), expiration_date, days_per_year)
//S(0) = B(0) + AI(0)
full_price = current_bond_price + accrued_interest_at_settlement
//FV(B(0)+AI(0)-PVCI)
contract_period = (expiration_date - settlement_date)/days_per_year
future_value = (full_price - pvci)*pow((1+risk_free_rate), contract_period)
//F(0) = FV(B(0)+AI(0)-PVCI) - AI(T)
adjusted_future_price = future_value - accrued_interest_at_expiration
//Q(0) = F(0)/CF
quoted_future_price = adjusted_future_price / conversion_factor
return quoted_future_price
}
current_bond_price = 108
face_value = 100
coupon_rate = 0.02
coupon_freq = 2
settlement_date = 2024.02.15
expiration_date = 2024.10.15
prev_coupon_date = 2024.01.15
risk_free_rate = 0.001
conversion_factor = 0.729535
quoted_bond_future_price = price_bond_future(
current_bond_price,
face_value,
coupon_rate,
coupon_freq,
settlement_date,
expiration_date,
prev_coupon_date,
risk_free_rate,
conversion_factor
)
print("The bond future price is: "+quoted_bond_future_price)