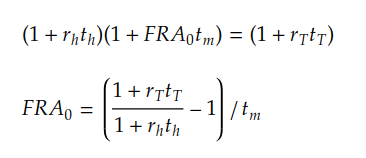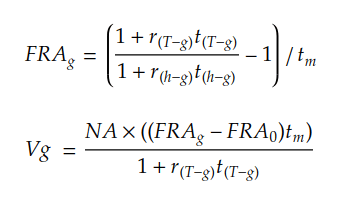In this blog series, I will aim to code the formulas and model algorithms covered in the CFA Level 2 program using Python and DolphinDB. Each topic will begin with a brief explanation of the formulas or algorithms, followed by their implementations in Python and DolphinDB.

This blog post focuses on pricing and valuing forward rate agreements (FRA). FRA is a forward contract on interest rates, established between two counterparties, a fixed interest payer (long), who is also the floating receiver, and a floating interest payer (short), who is also the fixed interest receiver. The long side incurs a gain and the short side incurs a loss when rates increases. FRA can be used to lock in the interest rate to hedge the risk of future borrowing or lending rates.

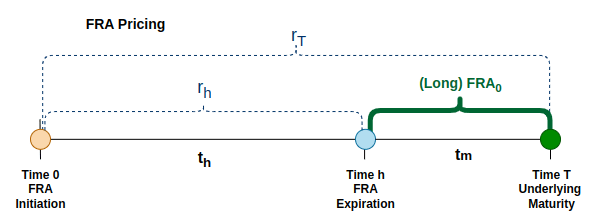
FRA Pricing

In the non-arbitrage approach, the Forward Rate Agreement (FRA) rate can be determined using the principle of no-arbitrage, which ensures there is no arbitrage opportunity between the spot market and the FRA market. when pricing FRA using non-arbitrage approach, we can build two portfolios:

1. Long FRA + short shorter period spot – long a forward agreement to borrow at the FRA rate settled at initiation (time 0), and simultaneously take an opposite position in the spot market for the short period (t(h)).
2. Long longer period spot – borrow in the spot market for the longer period (t(T)).

We need then equate the cost of those two portfolios (first line of the formulas below), and solve for the FRA rate (second line):

• FRA(0) – the rate agreed upon at initiation of the FRA
• r(h) – sport rate for the period towards the FRA expiration
• r(T) – sport rate for the period towards the underlying maturity
• t(h) – time period from the FRA initiation to the FRA expiration
• t(T) – time period from the FRA initiation to the underlying maturity
• t(m) – time period of the underlying, t(m) = t(T) – t(h)

Here are the Python and DolphinDB code implementations of that formula.

Code – Python

def calculate_fra_rate(rate_h, rate_T, period_h, period_T):
    
    period_m = period_T - period_h
    
    fra_rate = (
                    (1 + rate_T * period_T) 
                        / (1 + rate_h * period_h)
                    - 1
                ) / period_m
                
    return fra_rate

rate_h = 0.015  
rate_T = 0.0175  
period_h = 6/12
period_T = 9/12 
fra_rate = calculate_fra_rate(rate_h, rate_T, period_h, period_T)
print(f"The FRA rate is: {fra_rate:.4f}%")

Code – DolphinDB

def calculate_fra_rate(rate_h, rate_T, period_h, period_T){
    
    period_m = period_T - period_h
    
    fra_rate = ((1 + rate_T*period_T)/(1 + rate_h*period_h)-1
                ) / period_m
                
    return fra_rate
}

rate_h = 0.015  
rate_T = 0.0175  
period_h = 6.0/12.0
period_T = 9.0/12.0 
fra_rate = calculate_fra_rate(rate_h, rate_T, period_h, period_T)
print("The FRA rate is: " + fra_rate)

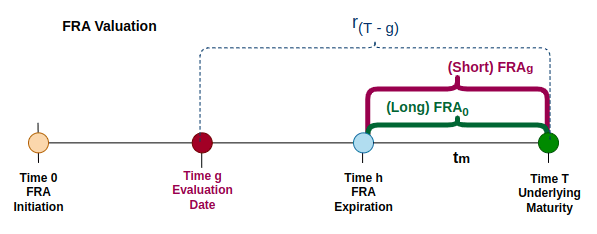
FRA Valuation

The valuation of an FRA is the process of determining its current value or the mark-to-market price. The value of an FRA at any given time comes from the difference between the rate you’ve locked in (the fixed rate) and the current market expectations for future interest rates.

An FRA can also be valued using the non-arbitrage approach, where we build two portfolios:

1. Long FRA at initiation (time 0)
2. Short FRA at current time (time g)

The value of the FRA (at time g) can be calculated as the present value (at time g) of the difference between the locked in rate (FRA(0)) and current rate (FRA(g)).

• V(g) – the value of the FRA contract at time g
• FRA(0) – the rate agreed upon at initiation of the FRA
• FRA(g) – the rate evaluated at the time g
• r(h-g) – sport rate for the period from time g to the FRA expiration
• r(T-g) – sport rate for the period from time g to the underlying maturity
• t(h-g) – time period from the time g to the FRA expiration
• t(T-g) – time period from the time g to the underlying maturity
• t(m) – time period of the underlying, t(m) = t(T-g) – t(h-g)
• NA – notional amount of the FRA contract

Code – Python

def calculate_fra_value(fra_0, rate_h, rate_T, period_h, period_T, notional_amount):
    
    period_m = period_T - period_h

    fra_g = calculate_fra_rate(rate_h, rate_T, period_h, period_T)
    
    fra_rate = (
                    notional_amount*(fra_g-fra_0)*period_m
                        / (1+rate_T*period_T)
                )
    
    return fra_rate

fra_0 = 0.00877
rate_h = 0.0125 
rate_T = 0.0135
period_h = 3/12
period_T = 6/12 
notional_amount = 10000000
fra_rate = calculate_fra_value(fra_0, rate_h, rate_T, period_h, period_T, notional_amount)
print(f"The FRA value is: {fra_rate:.4f}%")

Code – DolphinDB

def calculate_fra_value(fra_0, rate_h, rate_T, period_h, period_T, notional_amount){
    
    period_m = period_T - period_h

    fra_g = calculate_fra_rate(rate_h, rate_T, period_h, period_T)
    
    fra_rate = notional_amount*(fra_g-fra_0)*period_m / (1+rate_T*period_T)

    return fra_rate
}

fra_0 = 0.00877
rate_h = 0.0125 
rate_T = 0.0135
period_h = 3.0/12.0
period_T = 6.0/12.0 
notional_amount = 10000000
fra_rate = calculate_fra_value(fra_0, rate_h, rate_T, period_h, period_T, notional_amount)
print("The FRA value is: "+fra_rate)

• Coding towards CFA